Regression Standard Errors, Translated Into English
Mostly, anyway
Well! Here comes ol’ standard errors. Good ol’ standard errors, how we hate them.
Standard errors are a sticking point in many a statistical application for students and practitioners alike. We’re told about them, we know they’re supposed to be important. We learn the formulae (or software commands) to calculate them, and perhaps how to put together a hypothesis test using them. And we learn that we almost certainly picked the wrong ones to calculate. But lost in this swirl is what standard errors actually are, and what it actually means to make different adjustments to our standard errors. Robust standard errors - robust to what exactly, and what does it mean to be robust to it?
This page goes through what standard errors are, in a linear regression context, with an aim at translating the entire concept into English. There will be a little math, but only where it’s truly helpful.
Throughout, wherever I do refer to math, it will be in reference to the following model that we might use for our regression:
noting that everything here still works if you have more than one predictor in your model (although the calculations would need matrix algebra).
Standard Errors Describe how Regression Coefficients Vary from Sample to Sample
If you gather a data point, say, how tall someone is, you’ll get one value. If you gather another data point on another person, you’ll get another value. If you do this for a bunch of people you can see the data following a distribution. Perhaps this variable is distributed according to the normal distribution, or some other distribution. Every variable follows some distribution.
If you gather a bunch of random data points, say, how tall 100 people are, and how much they weigh, and you regress one of the variables on another, you get a single regression coefficient. If you do this again, you’ll get a slightly different regression coefficient, since you’ll randomly pick a different set of 100 people. Do this over and over and over again, getting a different random set of 100 people each time, and you’ll see your coefficient following a distribution.
Just like a variable follows a distribution, statistical estimates (such as a regression coefficient) follow distributions too. We call these sampling distributions.
We happen to know, by mathematical proof (and a few additional assumptions), that as long as we have a decent sample size, the particular sampling distribution that an OLS coefficient is a normal distribution. Normal distributions are defined by their mean and standard deviation.1 We call that standard deviation a standard error. Why an error? Because unlike in the distribution of height, where the mean may be typical but it isn’t, like correct, we think that the mean of the sampling distribution is what we want, and any deviation from that is thus in error.
So, the standard error is the standard deviation of the distribution you get if you estimate the same regression coefficient over and over again in a bunch of different random samples. The standard error is a description of this sampling distribution.
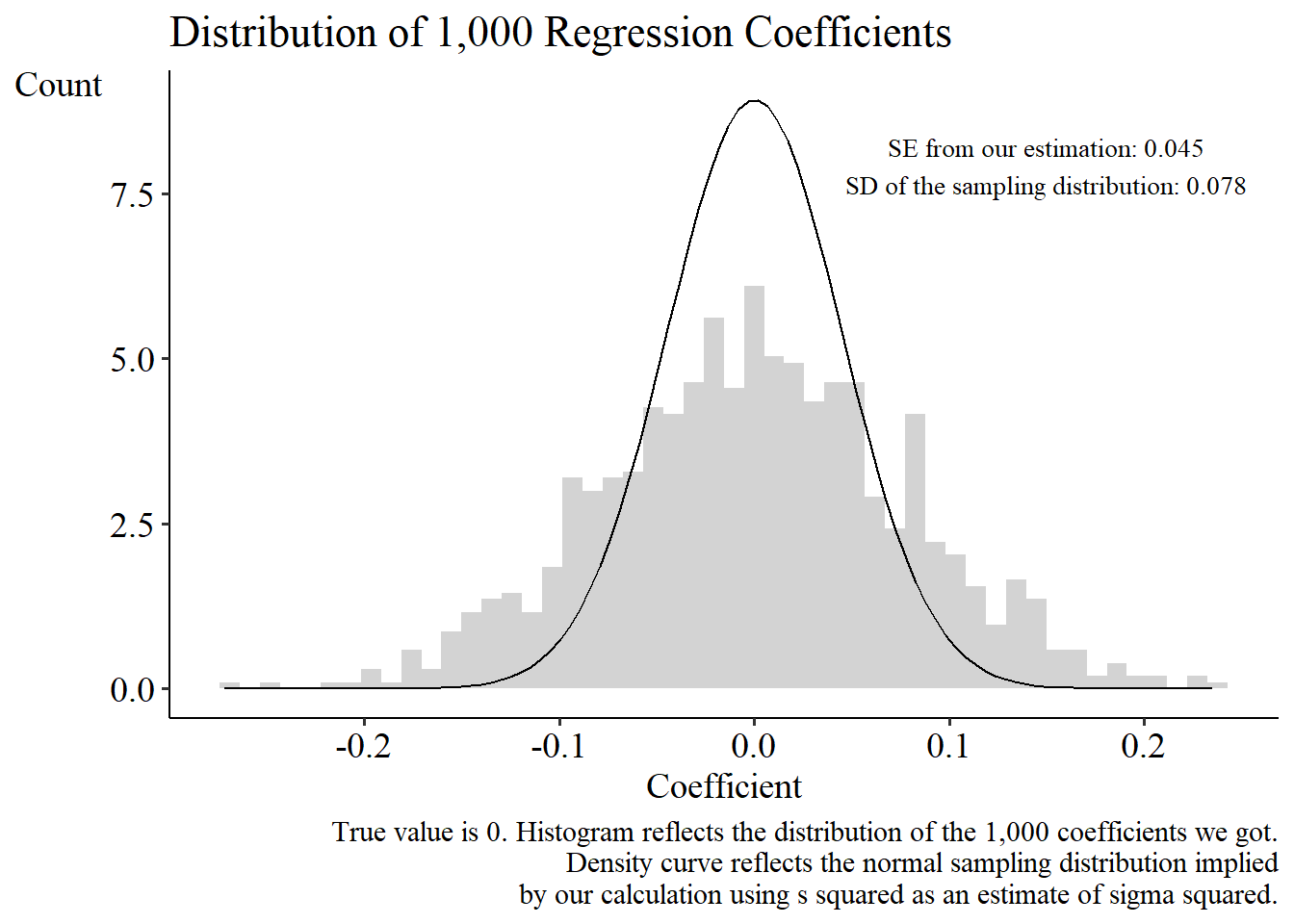
For an example, see the graph below. I generated 500 observations of X and Y, regressed Y on X, stored the slope coefficient, and then did it again and again, a thousand times. Obviously, I don’t get the same estimate every time, I get a distribution.
Knowing about this sampling distribution and its standard deviation is useful because knowing whether the sampling distribution is wide or narrow can tell you whether the single estimate you do have from your one-and-only sample is very likely to be near the mean (if the distribution is narrow with a small standard error, not often the apple falls far from the tree), or not that likely (if the distribution is wide with a big standard error, then your single estimate has a pretty good chance of being far from the mean, so who knows if you happened to end up far or near).
The standard deviation of this distribution is (an approximation of) the standard error of my regression coefficient.
Wait, just an approximation? Uh oh.
We Can Only Estimate the Standard Error
We want to know about our coefficient’s sampling distribution. That’s the only reason we care about the standard error at all.
However, all we can really prove about the distribution is that it’s normal (under some conditions). We know also that the mean of that normal distribution is the population value of the coefficient.
But we don’t know what that population value is! And we also don’t know what the standard deviation of that normal distribution is, either.
You might have learned in a classroom that you can get the standard error using the formula2
where σ squared is the variance of the error term ε.
This equation makes a lot of intuitive sense. The variance of the error term can be thought of as “how much stuff is going on in Y other than the influence of our predictors?”, in other words, noise. The more noise there is, the harder it is to precisely estimate things, and the standard error gets bigger. Also, the more X moves around, the easier it is to check whether Y happens to be moving around in the same way, and the more confident we can be in our estimate. So a bigger Var(X) leads to a smaller standard error.
But, guess what? We can’t observe the error term. We can observe the residual (Y minus the predicted value of Y), but the error term is Y minus the predicted value of Y we would get if we had an infinitely sized sample to estimate our model. We don’t have an infinite sample. So we can’t see ε. So we can’t actually calculate its variance σ squared (we can’t exactly calculate Var(X) for that matter, since we only have our sample of X’s, not an infinite number). We have to estimate it instead.
How We Estimate the Standard Error
Finally, an easy one.
Sure, we can’t see ε. But we can see the residual r, which is the difference between the outcome and our prediction. And it turns out r is a decent estimation of ε. So taking the variance of r (and then scaling it a bit), which we call s squared, is a decent estimate for σ squared. Similarly, the variance of r estimated using the data in our sample is a decent estimate of the variance of ε you get using an infinitely sized sample.
So we will never know the actual standard error, but we can make a good estimate by dividing the variance of the residual by the variance of X.3
At least we can as long as the variance of r is a good estimate of the variance of ε but that’s probably fine ah hell that’s gonna be the next secti
I Guess We Can’t Actually Estimate the Standard Error
In using the (slightly scaled) variance of r in place of the actual variance of ε that we want, we’ve made an assumption that the errors ε are spherical which is a cool way of saying that every single observation is a tiny little identical island. Every error term follows the same distribution (errors are identically distributed), and if you managed to learn what one of the error terms was, it would provide you no information about the others (errors are independent).
If this is not true, then our plan of using the residuals to stand in for the errors doesn’t work so hot.
We can see this in action. Let’s make 1,000 regression coefficients again, but I’ll make the data a bit differently. Previously X and Y were completely unrelated variables. Now, they’re still uncorrelated with each other (knowing X tells you nothing about the mean of Y, and so the true model is Y = 0*X + ε, and the true coefficient on X is 0), but now the variance of ε is bigger for bigger absolute values of X.
Those distributions don’t match! We’re trying to use our calculation (reflected by that density curve line) to approximate the actual sampling distribution (reflected by the histogram). But there’s clearly more variability in the actual sampling distribution than in the one we estimated. We’re doing a bad job estimating the actual sampling distribution!
Our estimate of σ squared is bad. So our estimate of the standard error is bad. So our estimate of the sampling distribution is bad, and all that nice statistical inference we wanted to do, or hypothesis tests we wanted to run, will be wrong.
What we really want to do, to estimate the variance of each observation’s error term separately. What’s the variance of the first observation’s error term? How about the second observation? Maybe they’re different. Let’s estimate what they are! We’d also want to estimate the covariance between the errors of every pair of observations. What’s the covariance between the first observation’s error term and the second observation’s? Between the second and the third? If we could do this, then we’d know exactly what σ squared is. Problem is, we can’t do that. We only observe each observation once. Can’t really estimate variance from that.
So if we want to properly estimate the standard error, we’ll need to strike a balance.4 We can allow for a little bit of violation, to avoid having to assume our errors are spherical, but we can’t go hog wild. If we assumed nothing about the correlations between error terms, we couldn’t estimate it.5 We gotta meet in the middle. So we’ll let the error terms be non-spherical, fine. But only in very specific ways!
Ways We Allow Errors to Misbehave
Alright, time to bring out the matrices. I promise it will be worth it.
In particular, we’re going to look at the variance-covariance matrix of the error terms. Let’s say we have six observations, and so a 6x6 matrix. It looks like this:
Each element tells you how two error terms are related. So ρ12 is the covariance between the first observation’s error term and the second. The covariance between a variable and itself is the variance, so along the diagonal we have variances, and so σ1 squared is the variance of the first observation’s error term.
When we assume those nice spherical error terms, we are assuming that the variance never changes (so all those σ squared 1, 2, 3, 4, 5, 6 values are all just the same σ squared), and also that none of the error terms are related to each other (so all those ρ values are 0).
Okay, so we can’t really work with the general matrix. But we think that the spherical one isn’t accurate. What else can we do?
Heteroskedasticity
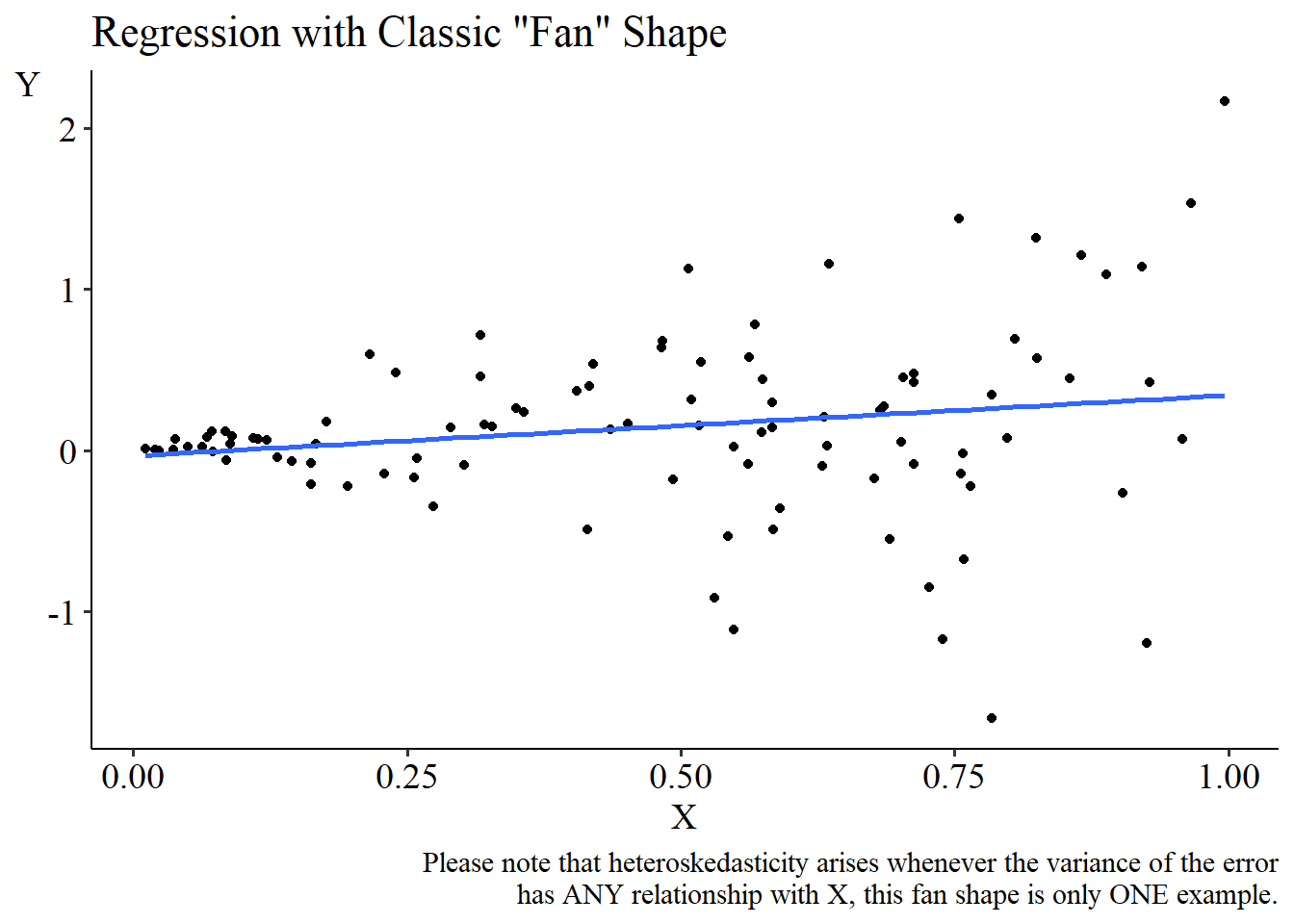
One common misbehavior we allow is heteroskedasticity. Like in the simulation in the previous slide, heteroskedasticity is when the variance of the error term differs across observations. It’s a particular problem when the way it differs is related to X. For example:
In this data, the residuals are quite tight around the OLS best-fit line on the left. The variance of the error term for these observations is likely to be small, since the residuals are small (which means that their squared values are small, so the variance is small). But as X increases, the residuals spread out. The residuals are bigger in absolute value, which means the error terms are also likely to be bigger in absolute value, which means their squares are bigger, so the variance is bigger. Less variance on the left, more on the right.
How might this occur in real life?6 Let’s say we’re studying personal finance and we want to know how your investments in stocks increase as your overall wealth increases, so we regress “Amount of Stocks” on “Overall Wealth”. For people with near-zero wealth, we can predict that they probably own near-zero stocks. That prediction is likely to be very accurate, so the errors will be small, with little variance. Among people with a lot of wealth though, they invest their money in different ways, so whatever prediction we make for, say, people who have a million dollars in wealth, some will have none in stocks, some will have a million dollars. We’ll be way off for some people, and in general there’s just a lot more noise. So the errors will be bigger in absolute value and we’ll have more variance.
We’re still assuming that the error terms are unrelated to each other. But we think the variance of each term is different. Our matrix now looks like this:
See what I mean by only allowing certain kinds of violations? We’re still forcing all those off-diagonal terms to be zero!
Clustering
Another allowable misbehavior is clustering. In clustering, your data exists naturally in different groups. And while we think that the nice spherical behavior we want happens between groups, when it comes to within groups it’s the wild wild west. We allow error terms to be correlated with each other as long as they’re in the same cluster.
Let’s say that we have two clusters in the data. Observations 1-3 are in one cluster, and observations 4-6 are in another. Our matrix now looks like:
Surprising, kind of, that working with a fully unrestricted matrix doesn’t work, but we can work with a bunch of fully unrestricted matrices that are unrelated to each other.7
When might this occur in real life? We might expect it any time your data can be organized into groups that we might expect to interact with each other, or share some sort of experience.8
For example, let’s say that we have a data set of students and we want to know the impact of teacher training on their test scores. So we regress student test scores on the amount of training their teacher got.
However, let’s say that we have a teacher who is very much above-average. Their students get much better test scores than you’d expect given the teacher’s level of training. All of those students have above-expectation test scores. Their errors are all similar. Knowing one student’s error term tells you information about what another student’s error term is likely to be, if you know they share a classroom.
But we can go a bit further. This makes it sound like clustering is the same as, say, a group-level effect. But let’s say we add a set of teacher-level fixed effects, controlling for the identity of the teacher.
Now, the fact that that one particular teacher is really really good is accounted for in the model and no longer in the error term. No more clustering, right? Wrong! For one thing, maybe that teacher is better at getting all their students to do well, so students in their class have more-similar test scores and thus lower variance in their error terms than students of other teachers. Alternately, if we have data on that teacher over many years of teaching, we’d still expect clustering. Maybe some years the teacher is grouchy and off their game. We’d expect all their students to do worse than expected that year, all at the same time. Knowing one student’s error tells you about another student’s error if they’re in the same class, and so they’re correlated.
Autocorrelation
The final kind of misbehavior we’ll allow is autocorrelation. Autocorrelation occurs when a given observation’s error term is correlated with another’s, and closer-together observations are more closely correlated.
“Closer together” could mean closer in time (temporal autocorrelation): an error term from 1995 is likely to be more similar to an error term from 1996 than it is to an error term from 2015. “Closer together” could also mean closer in space (spatial autocorrelation): an error term from my house is likely to be more similar to the error term for my neighbor’s house than it is to the error term from the house of someone living in Australia.
Autocorrelation pops up all the time whenever there’s data where the concept of proximity makes any sense - data with a time element like time-series or panel data, or geographically based data. Things, including errors, tend to spread from one observation to the next!
One really obvious place where this pops up is in how economic indicators change over time. Here’s the United States unemployment rate:
If we regress unemployment on month to estimate a time trend, we can clearly see autocorrelation.9 There tend to be long periods where the residuals are all positive, followed by long periods where the residuals are all negative. Telling you the value of one of the residuals gives you a pretty decent idea as to what the next one will be like.
What does the matrix look like? Depends how far we’re willing to go. We could say that each observation’s error term is correlated with the single closest observation (in a time-series context, with the single period before, and with the single period after). In the following matrix, we figure that the six observations are in chronological order, with the first observation for period 1, the second observation for period 2, and so on.
In this matrix, each observation’s error has its own variance term. We also allow each error to have a covariance of ρ with the single nearest observation.
But why stop there? Why not the two closest observations in either direction? Or three? The further we’re willing to go, the less precise we’ll be able to get about what we’re seeing (since who knows if the variation we’re seeing is real or just the echo of some far-off other observation?), but perhaps we need that to fairly reflect what’s going on!
Here we allow each error term to have one covariance ρ1 with the observation nearest to it, and a different, presumably weaker, relationship ρ2 with the next-nearest observation.
Correcting Misbehavior
So that’s what standard errors in regression are - they’re the standard deviation of the sampling distribution we’d like to know about. We can’t know the standard error for certain, but we can estimate it. Estimating it, frustratingly, requires that we are willing to make some assumptions about how the regression error terms relate to each other.
So what then? Once we’ve made some assumptions, how do we actually perform the estimation?
I’m not going to get too deep into the weeds here. But the most common approach is to use a sandwich estimator. Sandwich errors start with that calculation we left what feels like so long ago:
Our goal here was to estimate σ squared, right? But really that meant estimating the σ parameter in that variance-covariance matrix for spherical errors we just saw:
The reason we can collapse this to just σ squared in the equation is that it’s just that one parameter times this matrix that’s otherwise 1s across the diagonal and 0 elsewhere. In matrix algebra, that’s the “identity matrix” and it’s the equivalent of multiplying by 1 - you can just ignore it.
But if we think we have one of those other matrices, we can’t ignore it. But we can estimate all the parameters on it! So we go back to the old playbook and use the residual r to stand in for the error ε. Multiply together every set of residuals we have and get this thing:
OK fine, that’s a monstrosity. But we’re almost done. With this thing in hand, we hold it up against the variance-covariance matrix we think it should look like, and pick parameters that match this thing.
Think the errors are spherical? Then all those off-diagonal r1r3 values should be 0 - we can ignore them - and all the diagonal r1 squared elements should be the same. What would make our σ squared match this matrix? Pick a σ squared that starts by averaging all those diagonal elements together!
Think there’s clustering? Allow more elements to be non-zero and pick, for example, σ1 and ρ values that look like the diagonal r1 squared and off-diagonal r1r2 values we see. Similar idea for heteroskedasticity and autocorrelation - we’re picking what parts of the matrix are non-zero and any other restrictions on them, and then estimating the non-zero elements of the matrix in order to make them look like the r1 squared and r1r2 numbers we can actually calculate.
There’s more detail here,10 and this Wikipedia page gives a more thorough walkthrough that’s a bit more technical but also fairly friendly. But that’s the basic idea.
Now, to be clear, this is not the way you calculate standard errors to account for misbehavior. Sandwich estimators are just a way to do this. In many circumstances they aren’t even the best. There are many ways to estimate standard errors, even after deciding exactly how we think the variance-covariance matrix for the error terms looks. If you’d like to know more, I recommend my textbook chapter section on the topic.
Technically for this we must also assume that the error term is also normally distributed. However, there are a bunch of studies showing that, in practice, this isn’t actually all that important. Here is just one classic example. Unless the distribution of the errors is super non-normal, like it follows a power law or something, the resulting sampling distribution will be close enough to normal to just go with it.
Or its equivalent matrix form.
If you’re doing the matrix-algebra version where instead of /Var(X) you have (X’X) inverse, note that that’s conceptually the same thing! (X’X) is multiplying X by itself, i.e. squaring it, i.e. on your way to getting the variance. And taking the inverse just means “divide by”.
Alternately, some other kinds of estimation methods take a different approach. We’re trying to just do regular OLS here and produce a proper estimate of the standard error. But a method like Generalized Least Squares can, if you have a strong idea of exactly how the errors are non-spherical, actually produce a more precise estimate. Not just that it reports lower standard errors, but that it, as a method, produces better results that actually have a narrower sampling distribution.
We can get out of needing to estimate it in the first place using alternate standard error estimation methods like the bootstrap. But the bootstrap doesn’t just solve all our problems. Using a bootstrap properly does mean thinking about how you expect the error terms to be correlated with each other.
Economists tend to assume that heteroskedasticity is more or less always present. Can’t say that’s wrong!
Note that some approaches require a little better behavior, say by enforcing that all the σ values be the same within each cluster but allowing them to differ across clusters, or enforcing that all the ρ values be the same within cluster.
Although just because we might expect clustering in these cases doesn’t always mean we want to adjust the standard errors to account for it. See this neato paper.
And heteroskedasticity, for that matter. Not only does the overall variance of the residuals seem to increase quite a bit going from left to right, but on shorter timespans, variance is quite low during the periods where the trend is passing through the OLS line, and quite high when it’s far away. For that latter reason, heteroskedasticity can be assumed to pretty much always accompany autocorrelation.
Including the fact that when the errors aren’t spherical, we don’t actually get that nice clean
equation, since if the errors aren’t spherical, an earlier calculation step doesn’t cancel out and we’re actually calculating using this thing:
where that Ω is the variance-covariance matrix we’re trying to estimate. You can see how these two equations are related. If Ω were just a constant σ squared, we could slide that σ squared on out of that little space in the middle (the center of the “sandwich”) and we’d get X’X canceling out with one of its inverses, leaving just σ squared times the inverse of X’X (i.e. divided by the variance of X).