Controls in Difference-in-Differences Don't Just Work

Covariation, Violation, Frustration

I can’t help it. I have a compulsion. If I see the same mistake enough times, I have to write a helpful explainer.¹ And this one’s graced both my inbox and papers I’ve read or refereed enough times that it definitely qualifies. At the end of all of this, I’ll have a nice tidy link to send people the next time I get an email titled “Help with my DID model?” Here’s the basic problem:

If you want to use difference-in-differences (DID) as a research design (as many, many of us do), and you want to include covariates (control variables) in your analysis, you might think that you can just, well, do that, just like you’d normally do, and it will work. Toss ’em in your regression or do some matching.

But no! Actually, it doesn’t Just Work. And in fact it can mess you up pretty bad.

That’s not to say that you can’t use covariates with difference-in-differences. You can. But you need to do it in a way that’s specially designed to use covariates with difference-in-differences. This is not a novel observation, and some of the methods I’ll describe later that do let you include covariates have been around for decades, but often go unused in favor of just tossing some controls in a two-way fixed effects model or just sorta doing some matching.

This is much like the cavalcade of other disappointing things that have become much better-known about difference-in-differences in these recent years where social media has lubed the econometrics-to-applied-econometrics chute.² No, using your standard estimator for a staggered treatment difference-in-differences doesn’t Just Work. Using logit for a binary-outcome difference-in-differences doesn’t Just Work. Using a non-binary treatment for difference-in-differences doesn’t Just Work. Adding a time trend control to adjust for differences in prior trends doesn’t Just Work. Noticing your dependent variable is skewed and logging it to reduce the skew doesn’t Just Work. You can do difference-in-differences in all of these settings, but winging it on your own based on what doesn’t seem to cause issues in non-DID settings and seems to makes sense for your application (after all, none of these things break the logic of difference-in-differences as a research design, why would they break the estimator?) turns out depressingly not to function all that well.

So then, why would you even want covariates in your DID analysis, why doesn’t it Just Work, and if it doesn’t Just Work, then what works instead?

Throughout, we’ll use some fake data to demonstrate: in the province of Natex, the schools implemented a new training program for math teachers in the year 2000. The mostly-randomly-chosen schools A, B, and C got the training, and the schools X, Y, and Z never did. We have data from 1995 to 2005 are interested in whether the training program improved the normally-distributed 4th grade student test scores.

What Covariates in DID are For

Why would we even want covariates in a DID analysis anyway?³ What are the issues in a DID that covariates could solve?

First off, controls are not there for the same purpose that they serve in a typical attempt to identify a causal effect by controlling for stuff. You’re not really in the business of trying to account for differences between treated and control groups. The DID design sort of handles that part for you. By comparing how the treated and control groups change over time, any level differences between treated and control groups at the time that treatment was assigned are removed.

In place of an assumption about treatment assignment, we rely on the parallel trends assumption: if treatment had not occurred, the gap between treated and control groups would remain constant over time.

And that’s what controls are for. Not to help justify a conditional independence assumption, but to justify a parallel trends assumption. There are a few contexts in which you might think parallel trends doesn’t hold, but only because of some pesky measured variable that you could condition on, making parallel trends hold once again.⁴

How could this happen?

Let’s consider our treated schools A, B, and C, and our untreated schools X, Y, and Z. Let’s say that the X, Y, and Z schools serve areas that are a little wealthier.

Maybe Covariate Differences Make Trends Be Non-Parallel

Let’s also say that, over the same time period as our study, government funding for low-income students has been going way up, and the additional funding helps math scores.

Alternately, let’s say that, over the past few decades, math scores have just been increasing faster at lower-income schools than higher income schools, for no particular reason we can spot. They just are.

So, entirely absent our teacher training program, A, B, and C should have math scores increasing more quickly than at X, Y, and Z. Parallel trends fails, and if we estimate DID it will tell us the teacher training program is more effective than it actually was (since the training program will get the credit for the increasing trend among the schools it happened to treat). However, it fails for a reason we can measure: the income of the schools’ students. If only we could control for that, then we may be able to help parallel trends hold again.

Maybe Outcome-Affecting Covariates Change in Level

Let’s say that those higher-income students tend to get higher math scores than lower-income students, on average.

Let’s also say that, over time, A, B, and C have been attracting more high-income students. We’d expect scores to rise at the treated schools because the mix of students they attract has been changing towards students who tend to get higher scores.

So, entirely absent our teacher training program, A, B, and C should have math scores increasing more quickly than at X, Y, and Z. Parallel trends fails, and if we estimate DID it will tell us the teacher training program is more effective than it actually was (since the training program will get the credit for the increasing trend among the schools it happened to treat). However, it fails for a reason we can measure: the income of the schools’ students. If only we could control for that, then we may be able to help parallel trends hold again.

Maybe Outcome-Affecting Covariates Change in Importance

Let’s say that high-income students tend to get 10 more points on the math test than low-income students, on average.

Or, at least, they used to, in 1995. Due to changes in test-writing techniques, and perhaps some other changes, by 2005 high-income students are only expected to get 5 more point on the math test than low-income students, on average.

So, entirely absent our teacher training program, A, B, and C should have math scores increasing more quickly than at X, Y, and Z. Parallel trends fails, and if we estimate DID it will tell us the teacher training program is more effective than it actually was (since the training program will get the credit for the increasing trend among the schools it happened to treat). However, it fails for a reason we can measure: the income of the schools’ students. If only we could control for that, then we may be able to help parallel trends hold again.

Maybe We Expect More-Similar Groups to Have More-Similar Trends

Let’s say that of our low-income treated schools A, B, and C, C isn’t actually all that low-income. And of our high-income treated schools X, Y, and Z, X isn’t actually all that high-income.

We might very reasonably say that we expect math scores to be more similar between C and X than between the entire group of A, B, and C vs. X, Y, and Z. That’s the logic behind, well, the reason why we control for variables, or match on variables, most of the time.

Do we maybe also think that trends in math scores are going to be more similar between C and X than between the entire group of A, B, and C vs. X, Y, and Z? Note there’s no particular reason why “C and X have more-similar levels” implies “C and X have more-similar trends” but you can probably imagine why we might find the similar-trends thing plausible.

So we might expect that, if parallel trends doesn’t hold for any reason, we might have a better shot of it holding if we adjust in some way for income, making our DID model do more comparing of C vs. X as opposed to A, B, and C vs. X, Y, and Z.

Sometimes the Controls Themselves Don’t Work

One of the problems with trying to add controls to a DID analysis is that the estimators don’t do it in the right way. I’ll cover that in the next section. However, DID makes it so that a lot of controls aren’t going to work at all, no matter which estimator you use. You’re doomed from the start!

Picking the appropriate controls is never as simple as just tossing in everything that feels like it’s relevant. There are some controls for which adding them to your model makes things worse instead of better.

Bad controls pop up in difference-in-differences more often because the research design itself is set up such that more things become bad controls.

The most obvious of these is controls that lead to post-treatment bias. Post-treatment bias is what you get if you control for a variable that is itself affected by treatment. Imagine asking for the effect of the price of cigarettes on lung cancer rates… while controlling for the amount of smoking people do. More-expensive cigarettes likely lower lung cancer rates because they reduce smoking. Control for smoking and it will look like the price does nothing.

In the DID context, the treatment is applied at a certain period of time, going from off to on. This means that any control measured after the treatment is put in place is potentially itself affected by treatment.

So any control measured after treatment? Probably not a great idea! This is too bad because we might reasonably want to control for some of those. One of our schooling examples what “what if the lower-income schools see score improvements because they start attracting more high-income students at the same time the treatment went into place?” You really want to control for time-varying measures of income there! But what if it’s the treatment itself that’s making those new students join the low-income schools? Then part of the effect of the treatment is because it attracted different students. Control for income and you control away some of the real effect!⁵

For this reason, pretty much every approach to including covariates in a DID model explicitly recommends against using any controls measured after the treatment was put into place. Some software implementations make it impossible to do so. I do think it’s plausible that you could, in some cases, justify including these controls (if you were super duper certain that they were 100% only changing for reasons completely unrelated to treatment… but also are responsible for parallel trends violations). But in general you want to limit your controls purely to things you measure “at baseline,” before treatment occurs.

But even that doesn’t get us off the hook. In some pretty common contexts, covariates that change over time even if we only measure and match on them using their baseline values can get us in trouble.

This can occur because of regression to the mean, that pesky statistical phenomenon where, if something is much higher now than it normally is, then we’d expect it to decline pretty soon since, you know, it’s usually much lower than it is now, and will probably return there.⁶

This can get us into trouble. Say your treatment and control groups have very different levels of your covariate, like our schools, where the treated schools have lower incomes than the control schools. Then, you control for the baseline value of the covariate. What’s this going to do? It’s going to emphasize the highest-income treated schools, since those are the ones most like the the controls, and the lowest-income control schools, since those are the ones most like the treatment.

Or, rather, it will emphasize those based on the baseline-period values. Which is likely to be an unusually high-income period for the low-income schools we emphasize, and an unusually low-income period for the high-income schools we emphasize. Then regression to the mean kicks in, so we see the low-income school we emphasized become lower-income over time, and the high-income school become higher-income over time. This in itself will violate parallel trends. And yes, parallel trends is being violated because of a change in a measured variable, but only in the post-treatment values, and we don’t want to control for those!

We can see this occur in the below graphs. For simplicity, the way we’re implementing the control is by matching, picking the single treated-control matched pair with the most similar income value in 1999, the year before treatment.

This data is generated so that parallel trends holds without any controls, the control schools have income two units higher, which in turn is associated with scores .2 of a standard deviation higher, and income changes every period with a small random shock. I’ve set the true treatment effect here to be 0 to make it easier to spot what’s going on - we shouldn’t see any effect.

You can immediately see the problem on the income-picking side. Sure, we’ve picked schools B and Y as being the most similar in their baseline 1999 value. But both schools recede back towards the pack, giving incomes (and thus scores, which they influence) an upward trend for the untreated schools, and a downward trend for the treated schools, where no such trend exists in the full data.

It’s hard to see the impact on the estimate in just these six schools, and indeed the graph on the right doesn’t look that bad. But if I simulate this same procedure a thousand times and actually produce a DID estimate for the full and matched-only data, I get an average effect of 0.006 , pretty close to the truth of 0 I put in the data. For the analysis using the matched schools, I instead get an average effect of -0.482 , pretty far away from 0! And we can see why it’s negative, too: we expect the controls to regress back upwards to their higher mean after being matched especially low, and the treated group to regress back downwards after being matched especially high, leading the treated group to decline and the control to grow, making it look like the treatment reduces scores even though in truth it does nothing.

Thankfully, this regression-to-the-mean problem doesn’t always apply. It really only comes up if your covariate varies over time (whether or not the value you’ve chosen to match on is fixed in time), and the levels of the control and treatment groups are fairly different for that covariate. Covariates without big level differences between treatment and control on average aren’t affected by this, nor are covariates that are completely fixed over time.⁷

Really, you’re safest if you can stick entirely to covariates that are 100% fixed over time. Everything else at least has the potential for headache (and, uh, sometimes those have a potential for headache too, as I’ll discuss. Sorry).

Ways We Try To Make it Just Work

Alright, so we’ve limited ourselves to controls that are measured at baseline and not subject to regression to the mean, or, even better, controls that do not change over time. What estimators do we try to make Just Work?

One of them is matching. Matching different members of the treated and control groups together, and then performing DID on the matched subsets (or with the matching weights) seems okay. Maybe it does Just Work… assuming that the matching variables you’ve selected aren’t problem children of the kind outlined in the previous section.

The other is the usual suspect when it comes to things that feel like they should Just Work but don’t - the two-way fixed effects (TWFE) model, with a couple controls tossed in.

\(Y_{it} = \beta_i + \beta_t + \beta_1Treated_{it} + \beta_2Covariates_{it} + \varepsilon_{it}\)

We can already see how this might be at odds with our selection of good controls. Any covariate that doesn’t change over time is absorbed by the fixed effect. So… you’re already sort of controlling for all that. The additional covariates must either be of the time-varying variety, or at a finer level of detail than your fixed effects (perhaps you have fixed effects for schools, but time-fixed controls at the student level).

Or perhaps it’s salvageable? Let’s say that we’re either working with time-fixed covariates at a fine level, or we’ve found some time-varying covariates that we think are necessary to save our parallel trends assumption, and we’re super duper certain that they are not affected by treatment itself. Surely TWFE Just Works then, right?

Nope! Brantley Callaway provides a thorough explanation of the problems. The short of it is this:

1. For time-varying covariates, adding them to TWFE in effect means that you only control for the change in those covariates. If the reason you’re controlling for a variable is because you think the counterfactual path of the outcomes depends on the level of the covariate, you’re out of luck (even with the fixed effects!). More broadly, these regressions are highly sensitive to functional form; the outcome paths depending on initial values is just a common form of that.⁸

2. Time-invariant controls at a finer detail also don’t do what they’re supposed to here.

3. You end up with a strange treatment effect average. Your overall estimate will heavily reflect the effects of treated groups that have covariate values that are super uncommon relative to the untreated group.

The third is a bit tricky to demonstrate, so let’s leave that for another day, but let’s show the first two in action.

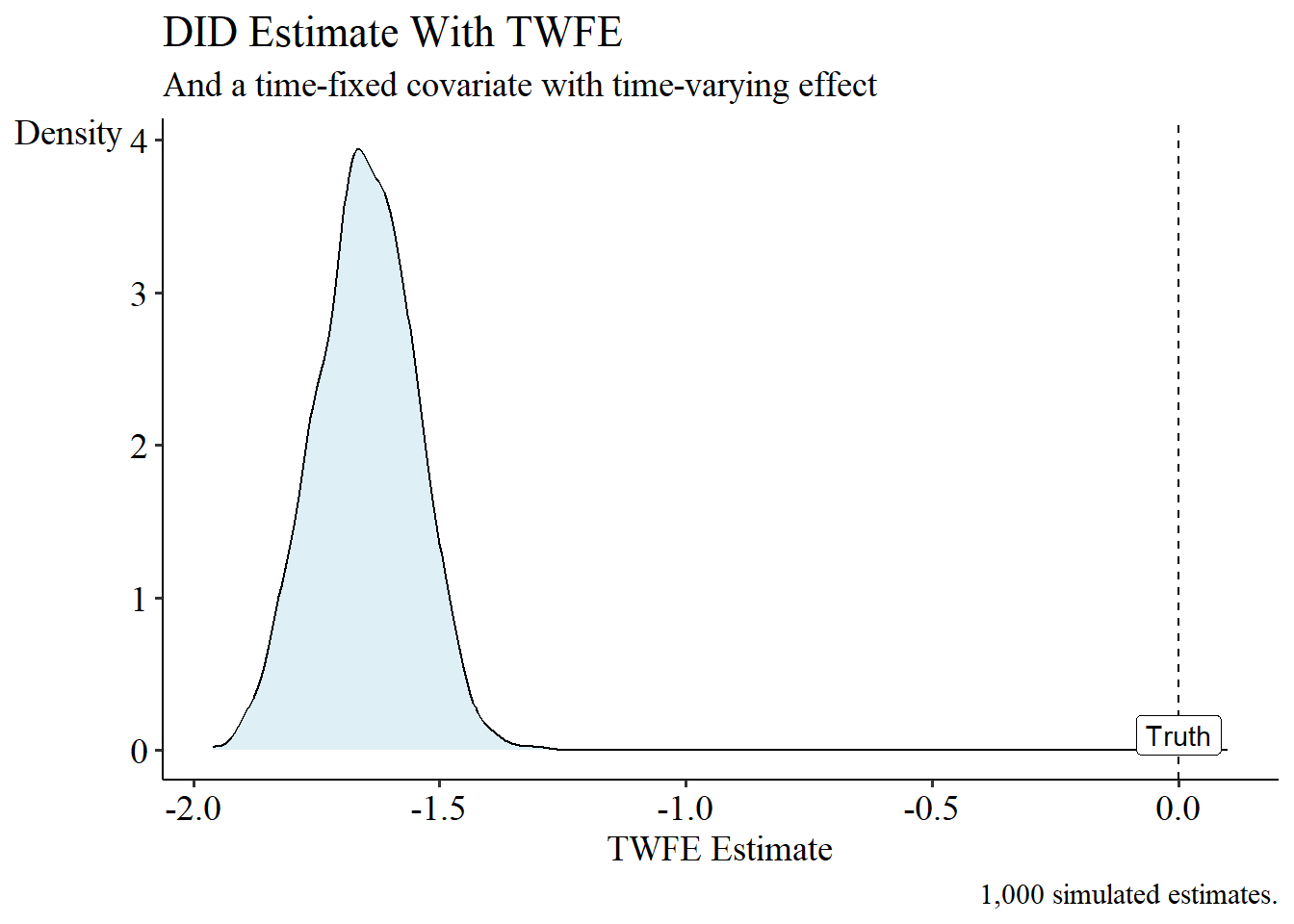
For (1), we’ll once again use Income as our covariate. As before, the treated schools are lower-income and the untreated schools are higher-income. I’ll also make the income level grow faster at at low-income than high-income schools, to include time-varying confounding. I’ll bake in a true treatment effect of 0. I’ll also bake in a violation of parallel trends only because of income. The true data-generating process for test scores is

\(TestScore_{it} = 0\times Treated_{it} + .1\times t + .1\times Income_{it} + .1\times Income_{it}\times t + \varepsilon_{it}\)

And the regression equation used to estimate the effect is

\(Scores_{it} = \beta_i + \beta_t + \beta_1Treated_{it} + \beta_2Income_{it} + \varepsilon_{it}\)

The distribution of estimates, across 1000 iterations, is:

That doesn’t look great, does it? And remember, that’s with a control that differs by treated group but is not affected by the treatment, so there’s no inherent post-treatment bias!

How about with time-fixed controls? Let’s try this two ways.

First, let’s revisit something I said earlier. I said that time-fixed covariates should be accounted for by the fixed effects. And that’s true… sometimes, depending on the reason why you need to control for them. Remember that case I mentioned earlier, where you might want to control because different levels of a variable imply different trends? Will the fixed effects account for that?

We already had that baked in to the simulation we just did, but maybe the only problem was the other stuff. Let’s take it out. Income is now completely fixed over time. So it’s no longer a control in our TWFE, but the difference in levels is handled by the school fixed effect. Will this handle the difference in trends that implies?

Not so good!

When thinking about whether controlling for pre-treatment covariates works, you need to be sure that this actually accounts for the reason why the covariate violates parallel trends. If, conditional on pre-treatment covariates, the covariate itself doesn’t show parallel trends, or if the effect of the covariate mutates over time, pre-treatment conditioning probably won’t work, just like it doesn’t work here.

Now let’s consider the other case. We’ll have time-fixed covariates that occur at a finer level of detail. Our fixed effects are for schools, but what if we have observations of students, 1,000 per school? The students present may change over time (if they don’t then this covariate will also be fixed at the school level and drop out), but each student’s covariate remains fixed. We can add that as a control. We’re assuming of course that the change over time in the value of the controls is completely unaffected by treatment, which is a strong assumption in a real setting!

In this case, we’re in a situation where parallel trends is again threatened entirely because of Income (which we’ll make a broad binary indicator for high/low income that is fixed within student) because high-income students keep joining the low-income schools at a faster rate than at the high-income schools.

That… actually seems to work okay! But that tail… and it’s super unstable. Does the time-fixed covariate have a time-varying effect as opposed to just time-varying levels? We’re right back at that last simulation. Are the levels of the time-fixed covariates changing because of treatment? Post-treatment bias! There are some other functional form restrictions we could break to make this not work too! May be better just to stay away.

How Does It Work if it Doesn’t Just Work?

Please don’t let the message of this article be “That old way doesn’t Just Work, but this new way Just Works!” It sorta seems like nothing Just Works in difference-in-differences. It feels like it should - the simplicity of the design, the most basic 2x2 version implemented in a nice tidy regression-with-an-interaction-term, and our previous experience with the TWFE model, makes it feel like it’s the kind of thing that Just Works. But going outside that very narrow range of applications, we learn that our freedom runs out very quickly.

None of the options in this section Just Work for every context. You have to study them and make sure they apply to your context. This is probably a good idea regardless of what research design or estimator you’re going with.

In particular, it’s very important to pay attention to what parallel trends means in the context and estimator you’re looking at. Parallel trends feels like a theoretical causal assumption that either holds for your research design or not. But it’s also a functional form assumption, and the thing you actually need to assume is true depends on things like “how is the data transformed?” or “what estimator are you using?” or “are covariates included?” If you’re doing any kind of DID other than plain-ol-linear-model-with-no-covariates-and-non-staggered-treatment, then you need to read up on what version of the parallel trends assumption you need to satisfy in your context, and think carefully about whether you do.

However, I will let you know about a couple of well-known approaches that allow you to incorporate covariates in a way that doesn’t fall prey to many of the problems outlined in this post. In fact, you may have already heard of the first two, which are already well-known for their ability to handle difference-in-differences with staggered treatment. The people who thought carefully about how to do that also thought carefully about how to add controls.

The first is the Callaway and Sant’Anna (2021) estimator, which has packages available in R, Stata, and Python. This estimator (usually) applies controls using matching. It performs the matching using only base-period covariates. This avoids using any covariate measured after treatment. The approach also allows for different levels of the covariates to predict different trends, accounting for the thing we wanted controls for time-fixed covariates to do in TWFE but it didn’t.

The second is the Wooldridge (2021) extended two-way fixed effects estimator (ETWFE),⁹ which has packages available in R and Stata. Turns out a lot of the problems with using TWFE to estimate DID can be solved by firing a giant cartoon cannon labeled “interaction terms” at the problem until it gives up and agrees to estimate your parameter. ETWFE incorporates covariates using a Mundlak device, where each group’s pre-treatment covariates get averaged over time, and then added to the model, plus (who could have guessed) some interaction terms with them.

Both of these estimators require that the covariates in question are measured “at baseline”. Both directly address the question of what happens when initial covariate differences generate differing trends over time. A main difference in how covariates are handled is that Callaway & Sant’Anna allows a bit more flexibility in covariates that change over time before treatment (at least in cases where there’s staggered treatment and thus more than one “baseline” period), rather than averaging everything out. Callaway & Sant’Anna also use matching, as opposed to regression in Wooldridge, so many of the typical differences between the two approaches pop up there.

So how about time-varying covariates. Are you out of luck? Does the likelihood of post-treatment bias make the whole task a fool’s errand? Even in cases where we know we don’ have post-treatment bias, are we out of luck on estimators!

Perhaps not! One new method worth looking at is Caetano, Callaway, Payne, and Rodrigues (2022), which focuses on the two-period case and has a helpful explainer available. There’s no package yet, but given Callaway’s history I wouldn’t be surprised if one appears before too long. It basically offers a way to adjust for time-varying covariates in a way that does not rely nearly so heavily on the linearity of the model. And while it isn’t a magic button that lets you control for things that are affected by treatment, it offers a peek in the door: it provides conditions under which you can control for things that are affected by treatment.

A hint at salvation! It might just work. But it won’t Just Work.

1. An edited version of this article will likely find its way into the difference-in-differences chapter of my book when I get around to a second edition. Some of this is already in there, but it’s really not as explicit as it should be. Not including something like this was one of my most immediate regrets of the first edition!

2. And to be entirely clear, I am primarily on the latter end of that chute and only sometimes on the former. I learned about many of these things right alongside you.

3. “Why are you controlling for that?” is too often an unasked question. Controls aren’t there just because! They serve a purpose. If you don’t need that purpose, or if you’ve chosen controls that don’t serve that purpose, then you don’t want those controls!

4. Another way to think about it is that, in regular practice, you want to control for things that are both related to treatment and related to the level of the outcome. In DID, you want to control for things that are both related to treatment and related to changes in the outcome.

5. In this case we might still say we’d want to control for income, as we might only want to count “improved the existing students” effects and be fine controlling away treatment effects that occur due to attracting other students. However, we’re still in trouble in this case because of the potential for collider bias. Controlling for income in this case could lead treatment to be correlated with some other determinant of why more high-income students are joining low-income schools that it wasn’t already correlated with. If that other determinant would be responsible for breaks in parallel trends, oops!

6. Regression to the mean can be a pest for DID in other non-covariate-related ways too, especially the well-known “Ashenfelter Dip”, where regression to the mean in the outcome is itself responsible for the violation of parallel trends. Say treatment is assigned on the basis of which schools have the lowest incomes in 1999. This is likely to pick off schools having below-average-for-them incomes in 1999, which are likely to regress to the mean, making the treatment look effective even when it’s not, due to parallel trends being violated.

7. Although if you think about it (or read the linked paper) you’ll realize that this problem does apply if we want to do things like control for, or match on, pre-treatment values of the outcome variable. Treatment and control have different levels of the outcome in the pre-treatment period? Then if parallel trends does hold you can break it by matching on pre-treatment outcomes, since you’ll pick away-from-mean outcomes that happen to be briefly more like the other group and are likely to drift back towards their means.

8. This is somewhat related to another thing that doesn’t Just Work, which is estimating a covariate-specific trend as a control (or subtracting that trend out).

9. Which, speaking of estimators that allow you to do a version of DID that doesn’t Just Work, has a follow-up paper that uses an extension of the method that works for DID in nonlinear models, y’know, since just doing TWFE in a logit doesn’t Just Work. The same R and Stata packages implement this nonlinear version.