Confounding Twins

A Successful but Pointless (?) Chalkboard Journey

Please note that Substack does not currently support in-line subscripts, which may make reading some of the in-line math a bit confusing. I’ve tried to make it as clear as I can. Sorry!

Causal inference is full of hard truths. There are plenty of situations in which estimating a causal effect is just not feasible, and plenty of research designs that feel good but don’t actually work that well. And yet, I know that the toolbox isn’t full yet. There are more strategies out there to try! Every once in a while I’ll think of a strategy for causal inference that I haven’t seen before, or some sort of cheat code to get around some daunting assumption and I just can’t rest until I give it a whirl to see if it at least works in theory. My previous forays into this have often actually worked to one degree or another.¹

Today we’ll see how another one does, and as I write this, I promise to publish this whether it works or not.

My Confounded Twin

Let’s say we want to know the effect of some treatment X1 on some outcome Y. As you do. However, as you’ll be unsurprised to learn, there is some confounder W that affects both X1 and Y. Worse, we can’t measure W in order to adjust for it. A story as old as time.

However, what if there is another variable, a twin, X2, that shares the exact same confounding problem?

We might have been tempted to solve a problem like this in other contexts without thinking about it too hard by just regressing Y on X1 while adding a control for X2, using X2 as a proxy for W, since they’re clearly closely related. But while this shuts down one confounding path, this clearly leaves open another, X1←W→Y. It will (probably) reduce the confounding problem but not eliminate it.

But maybe there’s something else we can do in this situation where we have twin variables that are confounded in the same way. Let’s start from the simplest case. Let’s say that that X2→Y arrow actually has a weight of zero, and that everything is nice and linear so we have the data-generating process:

\(X_1 = \beta_0W+\varepsilon_{X_1}\)

\(X_2 = \alpha_0 W + \varepsilon_{X_2}\)

\(Y=\gamma_0W+\gamma_1X_1+\varepsilon_Y\)

where all the εs are unrelated to each other, If we just regress Y on X1, what do we get? By the standard omitted variable bias formula we get

\(E(\hat{\gamma}_1) = \gamma_1+\frac{\gamma_0\beta_0\sigma_W^2}{\beta_0^2\sigma_W^2+\sigma_{\varepsilon_{X_1}}^2}\)

where σ represents the standard deviation of the thing in the subscript. Alright, now how about if we regress Y on X2? Doing some simple swapping out of terms to get the formula I had in my head when I started out on this idea (which will come back to bite us later) we get:

\(E(\hat{\gamma}_2) = \gamma_2+\frac{\gamma_0\alpha_0\sigma_W^2}{\alpha_0^2\sigma_W^2+\sigma_{\varepsilon_{X_2}}^2}\)

Except keep in mind that the true effect of X2 on Y is 0. Let's also scale down X2 so that it has the same variance as X1 and make an additional assumption: that W doesn't just affect both X1 and X2, but once they're on the same scale it affects them to the same degree so that α0 = β0.² In that case we're getting

\(E(\hat{\gamma}_2) = \frac{\gamma_0\beta_0\sigma_W^2}{\beta_0^2\sigma_W^2+\sigma_{\varepsilon_{X_1}}^2}\)

That's exactly the bias term! So if we regress Y on X1 and subtract out what we get from regressing Y on X2, we will end up with the causal effect of X1 on Y without having to observe the confounder W.

Conceptually this is sort of similar to what happens with the control group in a difference-in-differences design. We want to see how treatment affects the outcome for a treated group, but time is a confounder. However, if we assume that the time confounder affects the control group in the exact same way it would have affected the treated group, then we can just subtract out the control group's time change from the treated group's time change to adjust.

Does This Actually Work?

Let's just do a quick check to see if this works, and just to give it a hard time let's compare it to some other obvious things we might do in this context.

I'm going to randomly generate some data according to the data generating process in the last section. W and all the εs will be generated as normal random variables with means 0 and standard deviations 1. All the parameters α, β, and γ will be set to 1, with the exception of our main treatment effect γ1 which will be set to 2. I'll generate samples of, let's say, 1,000 observations each, and then implement the strategy of regressing Y on X1 and subtracting the slope estimate I get from regressing Y on X2. I'll do this 2,000 times. What sampling distribution do I get for my estimate of the effect of X1 on Y?

Oops. We get an estimate centered around 1, not the correct answer 2. Just adding a control for X1, instead of doing subtraction, doesn't work either, producing an estimate of 2.33 (because controlling for a proxy can only do so much!). But it's better than 1 (and more precise too, which makes sense, since my method takes a difference of two estimators).

What Happened?

Let's revisit some of that perhaps-too-intuitive math, specifically where I derived what we identify when we regress Y on X2:

\(E(\hat{\gamma}_2) = \gamma_2+\frac{\gamma_0\alpha_0\sigma_W^2}{\alpha_0^2\sigma_W^2+\sigma_{\varepsilon_{X_2}}^2}\)

That term on the right is supposed to be the correlation between X2 and the error term, times the ratio of the standard deviation of the error term and the standard deviation of X2. However, I pretended as though, like in the derivation for γ1, that the only things in the error term were W and εY. But nope! Here's our Y formula:

\(Y=\gamma_0W+\gamma_1X_1+\varepsilon_Y\)

so if we regress Y on X2, then X1 will also be in the error term. Reworking our γ2 formula with this in mind gives us:

\(E(\hat{\gamma}_2) = \gamma_2+\frac{(\gamma_0\alpha_0 + \gamma_1\alpha_0\beta_0)\sigma_W^2}{\alpha_0^2\sigma_W^2+\sigma_{\varepsilon_{X_2}}^2}\)

Making the same simplifications as before (γ2 = 0, α0 = β0, σεX1 = σεX2) gives us

\(E(\hat{\gamma}_2) = \frac{(\gamma_0\beta_0)\sigma_W^2}{\beta_0^2\sigma_W^2+\sigma_{\varepsilon_{X_1}}^2} + \frac{(\gamma_1\beta_0^2)\sigma_W^2}{\beta_0^2\sigma_W^2+\sigma_{\varepsilon_{X_1}}^2}\)

So, that same bias–on-γ1 we so nicely got before… plus a nuisance term based on the contribution that X1 makes to the error term as well as X1's relationship to X2 via W. Worse still, that nuisance term contains γ1 in it. That's the very thing we were unable to identify before that led us down this path! So no hope in just calculating the nuisance term to remove it.³

Can We Save It?

Now, there's an obvious fix here, which is this: when getting our γ2 coefficient, just get it from a regression of Y on X1 and X2 instead of just X2 alone. With X1 controlled for, it moves out of the error term, so the nuisance term should go away and we're golden right?

Well, no. Without working out the specifics of it, this won't work. By good ol' Frisch-Waugh-Lovell we know that adding X1 as a control is equivalent to using OLS to predict Y and X2 with X1 and subtract out those respective predictions. But since W is still in the error term, the predictions we get will themselves not be reflective of the actual γ1 parameter we're trying to get rid of (or the "effect of X1 on X2", which is 0). So our result will continue to be biased.

We can confirm this doesn't immediately work by simulation without having to work out the exact formula.

This certainly looks a lot better, and now outperforms the basic approach of just regressing Y on X1 and X2 and taking the X1 coefficient. The bias now appears to be about 1/6 given these parameters.

OK fine, so, progress at least. Is it worth figuring out the actual formula to see if there's another step that can take us all the way home?

Fine.

Regressing Y on X1 and X2 gives us:

\(E(\hat{\gamma}) = \gamma+(X'X)^{-1}X'(\gamma_0W+\varepsilon_Y)\)

where X is a two-column matrix with X1 and X2 as columns and γ is a two-element vector representing the γ1 and γ2 coefficients on X1 and X2, respectively (recalling that γ0 is the coefficient on the omitted W variable). Through our independence assumption, that εY goes away and we have

\(E(\hat{\gamma}) = \gamma + (X'X)^{-1}E(X'W) \)

\(= \gamma + \begin{bmatrix}Var(X_1) & Cov(X_1,X_2) \\Cov(X_1,X_2) & Var(X_2) \end{bmatrix} \begin{bmatrix}\beta_0\sigma^2_W \\ \alpha_0\sigma^2_W \end{bmatrix}\)

\(= \begin{bmatrix} \gamma_1 \\ 0 \end{bmatrix} + \begin{bmatrix}\beta_0^2\sigma^2_W+\sigma^2_{\varepsilon_{X_1}} & \alpha_0\beta_0\sigma^2_W \\ \alpha_0\beta_0\sigma^2_W & \alpha_0^2\sigma^2_W+\sigma^2_{\varepsilon_{X_2}} \end{bmatrix} \begin{bmatrix}\beta_0\sigma^2_W \\ \alpha_0\sigma^2_W \end{bmatrix} \)

… huh. You know, it sure does look like if we do our standard simplifying assumptions of α0 = β0 after rescaling, then those two bias terms will be exactly the same. And since X2 in truth has no effect, our γ2 estimate will be exactly the same as our γ1 bias. We seem to have made it.

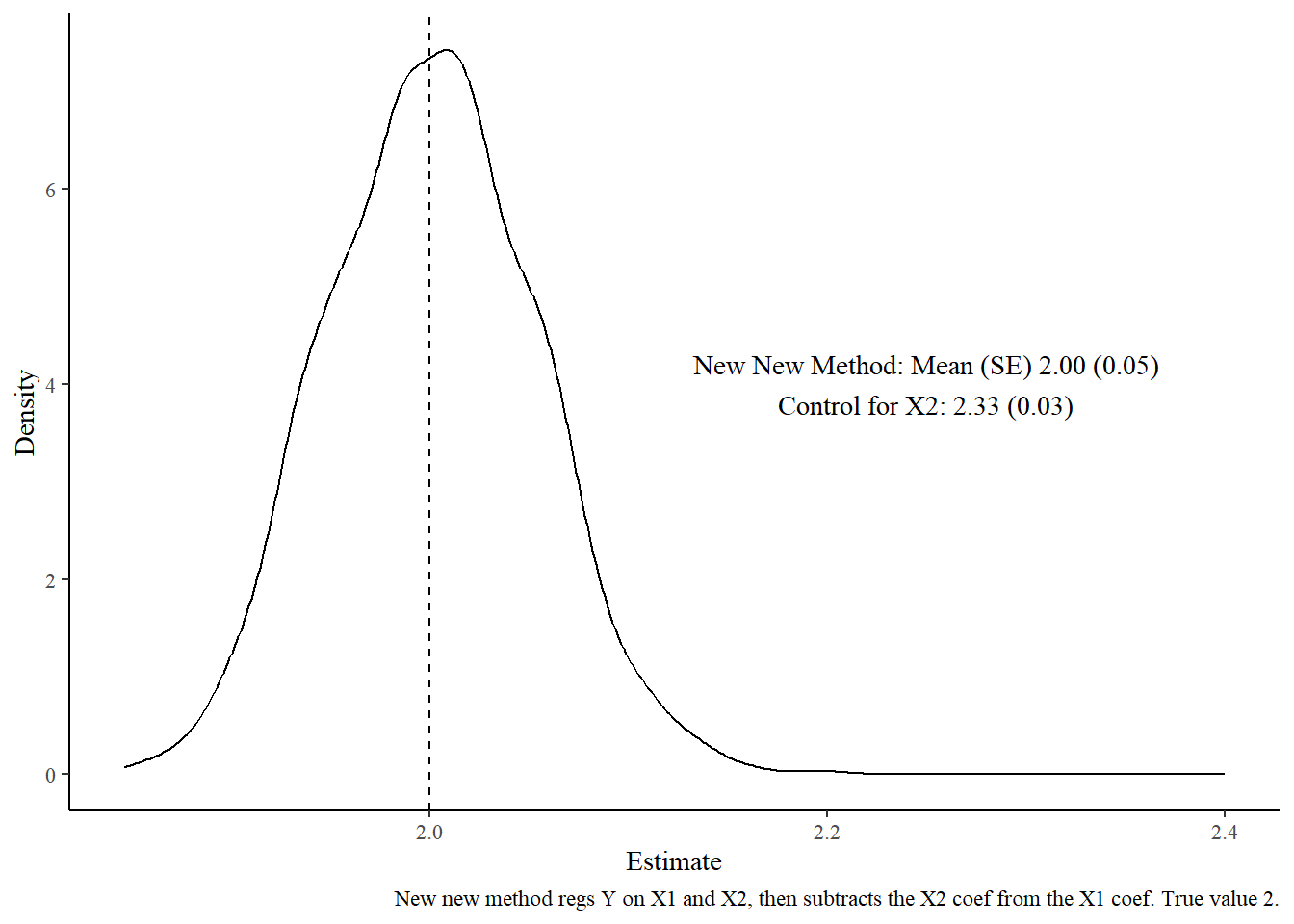
So does that work? Did I miss something? Let's run another simulation.

That looks bang on to me! By regressing Y on both X1 and X2 and then subtracting our X2 coefficient, which exactly represents the bias on the X1 coefficient, out of the X1 coefficient, we end up with the true causal effect of X2 on Y.

Success!

How Much Kidney Can That Twin Donate?

Or at least success in the very limited context of the pretty heavy assumptions I've put on the problem. I've assumed no effect of X2 on Y, and I've assumed identical effects of W on both twins after rescaling so both variables have the same variance.

How far can we get if that isn't true? Let's revisit our formula from the previous section.

\(= \begin{bmatrix} \gamma_1 \\ \gamma_2 \end{bmatrix} + \begin{bmatrix}\beta_0^2\sigma^2_W+\sigma^2_{\varepsilon_{X_1}} & \alpha_0\beta_0\sigma^2_W \\ \alpha_0\beta_0\sigma^2_W & \alpha_0^2\sigma^2_W+\sigma^2_{\varepsilon_{X_2}} \end{bmatrix} \begin{bmatrix}\beta_0\sigma^2_W \\ \alpha_0\sigma^2_W \end{bmatrix}\)

If we relax our γ2 = 0, α0 = β0, and σεX1 = σεX2 assumptions (keeping in place our "no other relevant variables" and "linearity" assumptions - this is a blog post, not a dissertation), then implementing the strategy I've settled on gives us an estimate for the effect of X1 on Y of

\(E(Effect of X_1 on Y) = E(\hat{\gamma}_1 - \hat{\gamma}_2) = (\gamma_1 + (\beta_0^2\sigma^2_W+\sigma^2_{\varepsilon_{X_1}})\beta_0\sigma^2_W + \alpha_0\beta_0\sigma^2_W\alpha_0\sigma^2_W))\)

\(- (\gamma_2 + \alpha_0\beta_0\sigma^2_W\beta_0\sigma^2_W + (\alpha_0^2\sigma^2_W+\sigma^2_{\varepsilon_{X_2}})\alpha_0\sigma^2_W)\)

\(= (\gamma_1 - \gamma_2) + \sigma^2_W((\sigma^2_{\varepsilon_{X_1}}\beta_0 - \sigma^2_{\varepsilon_{X_2}}\alpha_0) + \sigma^2_W(\beta_0^3 + \alpha^2_0\beta_0 - \alpha_0\beta_0^2 - \alpha_0^3))\)

Well that looks fun. At the very least, if we don't have a very believable estimate (or assumed estimate, like 0), for γ2, we're going to be stuck without exact identification. That said, you could maybe do some interesting partial identification if you can at least choose the sign of γ2.

How about all that other business? There are two main terms remaining in the bias, even after we set γ2 = 0:

\(\sigma^2_W((\sigma^2_{\varepsilon_{X_1}}\beta_0 - \sigma^2_{\varepsilon_{X_2}}\alpha_0))\)

which tells us that this method will leave us with bias that scales with how different, in absolute terms, the influence of W on both twins is - in terms of the direct effect, and with those variance terms coming in to check us if we attempt to rescale a variable so the direct effects are in fact the same. Scale X1 or X2 up or down so that the W effects actually are the same? Then those sigmas will scale in the other direction to offset.

The other term is:

\(\sigma^4_W(\beta_0^3 + \alpha^2_0\beta_0 - \alpha_0\beta_0^2 - \alpha_0^3)\)

which is a fun little tricky-to-interpret slice that tells us that the bias will also grow (and pretty quickly, we'd imagine, given those cubes) in how differently W affects X1 and X2. So this whole "twin" thing relies in concept on having a similar confounding structure for X1 and X2, but in practice it also relies on having a similar confounding size.

How much does this matter? I can't track all plausible ranges of α0 and β0 but over a limited range we can see the size of this part of the bias (assuming σW = 1):

You can see that, unless one of α0 or β0 is near 0 (which, if that's true, the rest of this method either doesn't matter or doesn't work for other reasons), this part of the bias gets pretty bad when deviating even a little from α0 = β0. Any sort of light color on this graph is a bias of around 10 or more, which is 5x the biggest effects of W on either X1 or X2 considered here!

Although maybe we could pull some weird rescaling tricks to try to make α0 = β0 so this quickly-growing thing goes away. Maybe the changing sigma values in the other part of the bias don't grow as quickly if we do this? Or given we have some cubics there maybe we could get lucky if one effect were positive and the other negative - maybe some cubes cancel out? Although we don't really see that on the graph. Who knows.

What We Get

So what did we get out of all of this? A fun little exercise, I think, for the most part. And a fun way to spend my father's day off (aside from the process of copy-pasting all this math into Substack. C’mon Substack, throw us math people a bone).

Also, a method for identifying a causal effect that is (at least to me) brand new. And in a very very narrow set of circumstances, it actually works.⁴ Hey, maybe someone sees this and figures out a way to make it work better. You never know.

1. Some of these working strategies have remained at the just for fun stage, some turning out publishable, and some turning out publishable… for someone else about ten years before I thought of it.

2. This ensures by extension that

\(\sigma_{\varepsilon_{X_1}}=\sigma_{\varepsilon_{X_2}}\)

since we've scaled X1 and X2 to have the same variance, and Wα0 now has the same variance of Wβ0, so the error terms must now have the same variance too.

3. At our very most optimistic we might note that the nuisance term has β0 squared in it. So if we suspect that α0 = β0 are below 1 and fairly small, then that nuisance term gets really small too. Of course, in that case, the confounding bias itself is already small. So I guess it takes a really really opportune situation and makes its already-not-very-biased estimate even slightly less biased. Woo hoo?

4. And if we're being honest, all causal inference methods only work in a narrow set of circumstances. The only questions are "how narrow?" and "can you actually tell whether or not you're in that circumstance when you are?".